Tháp tam giác
Bạn bị nhốt trong một tòa tháp tam giác vô hạn.
Tầng thứ \(k\) chứa đúng \(k\) phòng, được đánh số từ trái qua phải.
Mỗi phòng được xác định bởi cặp số \((w, e)\):
- \(w\): số tầng.
- \(e\): vị trí trong tầng (1 ≤ e ≤ w).
Từ mỗi phòng \((w, e)\), bạn có thể đi lên một trong hai phòng: \((w + 1, e)\) hoặc \((w + 1, e + 1)\).
Tuy nhiên, chỉ một hướng có sẵn:
- Nếu \(w + e\) là chẵn \(→\) đi được đến \((w + 1, e)\).
- Nếu \(w + e\) là lẻ \(→\) đi được đến \((w + 1, e + 1)\).
Tham khảo hình minh họa để dễ hiểu hơn:
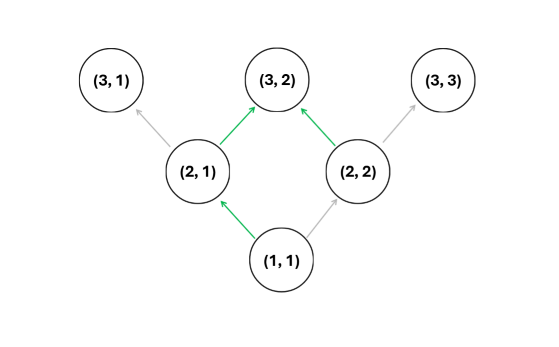
Ví dụ như trong hình:
- Có đường đi từ \((1, 1)\) tới \((3, 2)\).
- Không thể đi từ \((2, 1)\) tới \((3, 1)\).
Bạn bắt đầu tại phòng \((1, 1)\). Tại mỗi bước, bạn được chọn:
- Di chuyển theo đường có sẵn tốn \(0\) điểm sức mạnh.
Thay đổi đường đi của một phòng \((w, e)\):
- Đảo hướng có sẵn sang hướng còn lại. Nếu đường hiện tại từ \((w, e)\) tới \((w + 1, e)\) có sẵn thì bạn có thể chuyển con đường này thành \((w, e)\) tới \((w + 1, e + 1)\) (và ngược lại).
- Mỗi lần thay đổi tốn 1 điểm sức mạnh.
Cho danh sách \(n\) phòng cần ghé thăm, hãy tính tối thiểu tổng điểm sức mạnh cần thiết để đi từ phòng \((1, 1)\) và ghé qua tất cả \(n\) phòng, theo bất kỳ thứ tự nào.
Đầu vào
Dòng đầu tiên chứa số nguyên \(n\) \((1 \le n \le 2 * 10^5)\) - số phòng cần ghé qua.
\(n\) dòng tiếp theo, mỗi dòng chứa một cặp số \((w_i, e_i)\) biểu diễn phòng cần ghé thăm. \((1 \le i \le n, 1 \le e_i \le w_i \le 10^9)\)
Đầu ra
Một số nguyên duy nhất là tổng điểm sức mạnh tối thiểu cần để ghé thăm tất cả \(n\) phòng. Đầu vào đảm bảo luôn có đường đi giữa các điểm.
Giới hạn
\(10\%\) số test: \(n = 1\).
\(20\%\) số test: \(1 \le n \le 8, 1 \le e_i \le w_i \le 10^3\).
\(30\%\) số test: \(1 \le n \le 2000, 1 \le e_i \le w_i \le 10^6\).
\(40\%\) số test: Không có ràng buộc gì thêm.
Ví dụ
| Đầu vào | Đầu ra |
|---|---|
| 3 1 1 4 3 2 1 |
0 |
| 2 2 2 4 3 |
1 |
| 2 1 1 1000000000 1000000000 |
999999999 |
Comments