MAH là nhân việt chính trong game "MAH VS MAH". Anh là một con quái vật nhỏ màu xanh, anh có sở thích thăm bạn bè của mình ở phía bên kia của công viên. Tuy nhiên công viên vào buổi tối cũng có thể làm cho người như MAH sợ hãi. Vì vậy anh ấy yêu cầu bạn giúp đỡ.

Công viên có \(2^{n+1}-1\) ô vuông kết nối bởi các đường đi thành một cây nhị phân đầy đủ có độ sâu là \(n\). Lối vào công viên nằm ở ô vuông thứ \(1\). Lối ra của công viên nằm ở các ô \(2^n, 2^n + 1, ... 2^{n+1}-1\) và những lỗi thoát này dẫn thẳng đến nhà bạn của MAH. Mỗi ô vuông \((2 \le i < 2^{n+1})\) có đường đi tới ô vuông \(i/2\). Do đó, có thể đi từ lối vào đến bất kỳ lối nào ra bằng cách đi bộ dọc theo chính xác \(n\) con đường.

Để chiếu sáng các con đường vào buổi tối, chủ công viên đã lắp đèn dọc theo các con đường. Con đường dẫn từ ô vuông \(i\) đển ô vuông \(i/2\) có \(a_i\) chiếc đèn.

MAH rất sợ lũ nhện trong công viên, vì vậy anh ấy không muốn đi những con đường mà không đủ độ sáng. Anh ấy muốn tất cả các con đường dẫn đến nhà bạn mình đều phải có cùng độ sáng. Điều đó làm anh cảm thấy an toàn.

Anh ấy muốn bạn giúp cài thêm đèn vào các đường đi. Xác định tổng số lượng đèn nhỏ nhất cần thêm trên các đoạn đường để tất các các đường đi từ cổng công viên đến lối ra có cùng số lượng đèn. Bạn có thể thêm bao nhiều đèn vào mỗi con đường cũng được.

Input

Dòng đầu chứa số nguyên n \((1 \le n \le 10)\) là số lượng con đường từ cổng đến tất các các lỗi thoát.

Dòng tiếp theo chứa \(2^{n+1} - 2\) số từ \(a_2, a_3 ... a_{2^{n+1}-1}\) - là số lượng đèn trên mỗi con đường trong công viên. \(a_i (1 \le a_i \le 100)\) là số lượng đèn trên đường từ ô vuông \(i\) đến ô vuông \(i/2\).

Output

In số lượng đèn ít nhất cần thêm để MAH cảm thấy an toàn khi đến chơi với bạn.

Example

Input

2
1 2 3 4 5 6

Output

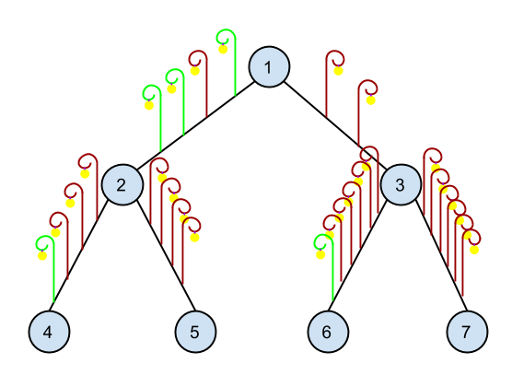
5

Xem hình dưới giải thích test case trên.